Uji Hipotesis Data Berpasangan

A.  Uji t untuk sampel Berpasangan

Uji-t berpasangan (paired t-test) adalah salah satu metode pengujian hipotesis dimana data yang digunakan tidak bebas yang dicirikan dengan adanya hubungan nilai pada setiap sampel yang sama (berpasangan). Ciri-ciri yang paling sering ditemui pada kasus yang berpasangan adalah satu individu (objek penelitian) dikenai 2 buah perlakuan yang berbeda. Walaupun menggunakan individu yang sama, peneliti tetap memperoleh 2 macam data sampel, yaitu data dari perlakuan pertama dan data dari perlakuan kedua. Perlakuan pertama mungkin saja berupa kontrol, yaitu tidak memberikan perlakuan sama sekali terhadap objek penelitian. Misal pada penelitian mengenai efektivitas suatu obat tertentu, perlakuan pertama, peneliti menerapkan kontrol, sedangkan pada perlakuan kedua, barulah objek penelitian dikenai suatu tindakan tertentu, misal pemberian obat. Dengan demikian, performance obat dapat diketahui dengan cara membandingkan kondisi objek penelitian sebelum dan sesudah diberikan obat. Contoh kasus lain misalnya program diet dimana pengukuran berat badan ditimbang sebelum dan setelah diet. Contoh lain yang bisa dianggap berpasangan meski terdapat 2 objek penelitian, misalnya perbedaan antara tinggi ayah dan anaknya.

Sebelum melakukan analisis data dengan uji-t berpasangan, terlebih dahulu kita uji apakah kedua data menyebar normal atau tidak. Statistik uji yang digunakan adalah Lilliefors (Kolmogorov-Smirnov) normality test.

Hipotesis uji normalitas:

·      H0 : Data menyebar normal

·      H1 : Data tidak menyebar normal

·      α = 0.05

Pada pengamatan berpasangan, (1) pemasangan antar sampel atau unit dilakukan sebelum percobaan dimulai berdasarkan harapan bila tidak ada pengaruh perlakuan maka kedua kelompok memberikan respon yang sama, dan (2) sumber keragaman dari luar dihilangkan, sehingga perhitungan nilai kritiknya didasarkan pada ragam perbedaan antar kelompok dan bukan pada ragam diantara individu dalam setiap sampel.

Contoh 1

Survey Kesehatan Nasional dan Pengujian Gizi yang diselenggarakan oleh Departemen Kesehatan dan Layanan Masyarakat, meneliti perbedaan antara tinggi yang dilaporkan sendiri dan yang diukur langsung dari beberapa wanita yang berusia antara 12-16 tahun. Data tinggi yang dilaporkan sendiri dan tinggi yang diukur disajikan pada Tabel di bawah ini :

1.    Apakah terdapat cukup bukti untuk mendukung dugaan bahwa terdapat perbedaan antara tinggi yang dilaporkan dan tinggi yang terukur dari wanita yang berusia antara 12-16 tahun? Gunakan taraf nyata 0.05.

2.    Buat selang kepercayaan dengan tingkat kepercayaan 95% antara perbedaan rata-rata tinggi yang dilaporkan dan tinggi yang diukur.

Contoh 2

Keefektifan dari suatu Bimbingan Belajar dalam menghadapi suatu Tes dinilai berdasarkan perbandingan antara nilai yang diperoleh siswa sebelum dan setelah melaksanakan kursus. Nilai tersebut diperoleh dari 10 siswa yang mengikuti Bimbel Tes Persiapan Masuk (based on data from the College Board and “An Analysis of the Impact of Commercial Test Preparation Courses on SAT Scores,” by Sesnowitz, Bernhardt, and Knain, American Educational Research Journal, Vol. 19, No. 3.)

1.    Apakah terdapat cukup bukti untuk menyimpulkan bahwa Bimbel efektif dalam meningkatkan skor (nilai ujian)? Uji pada taraf nyata 0.05.

2.    Tentukan selang kepercayaan 95% untuk perbedaan rata-rata antara sebelum dan setelah mengikuti Bimbel. Tuliskan pernyataan dan interpretasi hasilnya.

B.  Uji Hipotesis T-test pada SPSS

1.    Syarat Kelengkapan Data

Untuk melakukan Uji Paired Sample T Test, data yang digunakan harus berdistribusi normal. Sehingga hipotesis yang dibuat dapat dilakukan analisis dengan uji Paired Sample T Test.

2.    Penentuan Hasil Uji Paired Sample T Test

Uji Paired Sample T Test menunjukkan apakah sampel berpasangan mengalami perubahan yang bermakna. Hasil uji Paired Sample T Test ditentukan oleh nilai signifikansinya. Nilai ini kemudian menentukan keputusan yang diambil dalam penelitian. Nilai signifikansi (2-tailed) < 0.05 menunjukkan adanya perbedaan yang signifikan antara variabel awal dengan variabel akhir. Ini menunjukkan terdapat pengaruh yang bermakna terhadap perbedaan perlakuan yang diberikan pada masing-masing variabel. Nilai signifikansi (2-tailed) >0.05 menunjukkan tidak terdapat perbedaan yang signifikan antara variabel awal dengan variabel akhir. Ini menunjukkan tidak terdapat pengaruh yang bermakna terhadap perbedaan perlakukan yang diberikan pada masing-masing variabel

3.    Contoh Uji Paired Sample T Test

Digunakan contoh penelitian pada tutorial sebelumnya, yaitu "Peningkatan Kekuatan Otot Kelompok Perlakuan dengan Pelatihan Angkat Dumbell". contoh data paired sample t test

Data diatas adalah data hasil tes awal (point sebelum pelatihan angkat dumbell) dan test akhir (point sesudah melakukan pelatihan angkat dumbell). Data ini terdiri dari 15 sampel yang berdistribusi normal.

Berikut langkah-langkah melakukan uji Paired Sample T Test:

1.    Klik Analyze > Compare Means > Paired-Samples T Test tombol perintah uji paired sample t test

2.    Memasukkan variabel dari sampel berpasangan

Setelah kita melakukan langkah di atas, akan terbuka jendela Paired Samples T Test. Masukkan variabel dari sampel berpasangan pada kotak Paired Variable. Pada kolom Variable 1 masukkan variabel pada kondisi pertama (Contoh: Test Awal) dan Variable 2 masukkan variable pada kondisi kedua (Contoh: Test Akhir).

3.      Klik OK

Setelah kita klik OK, hasil analisis ditampilkan pada jendela output.

4.    Membaca Hasil Uji T Berpasangan

Berikut hasil output pada langkah di atas:

D1. Tabel Paired Samples Statistics

Tabel Paired Samples Statistics menunjukkan nilai deskriptif masing-masing variabel pada sampel berpasangan.

·      Tes Awal mempunyai nilai rata-rata (mean) 25.47 dari 15 data. Sebaran data (Std. Deviation) yang diperoleh adalah 2.588 dengan standar error 0.668.

·      Tes Akhir mempunyai nilai rata-rata (mean) 29.87 dari 15 data. Sebaran data (Std.Deviation) yang diperoleh 3.777 dengan standar error 0.975.

Hal ini menunjukkan tes akhir pada data lebih tinggi dari pada tes awal. Namun rentang sebaran data tes akhir juga menjadi semakin lebar dan dengan standar error yang semakin tinggi.

D2. Tabel Paired Samples Correlations

Tabel Paired Samples Correlations menunjukkan nilai korelasi yang menunjukkan hubungan kedua variabel pada sampel berpasangan. Hal ini diperoleh dari koefisien korelasi Pearson bivariat (dengan uji signifikansi dua sisi) untuk setiap pasangan variabel yang dimasukkan.

D3. Tabel Paired Samples Test

Tabel Paired Samples Test merupakan tabel utama dari output yang menunjukkan hasil uji yang dilakukan. Hal ini dapat diketahui dari nilai signifikansi (2-tailed) pada tabel.Nilai signifikansi (2-tailed) dari contoh kasus ini adalah 0.001 (p < 0.05). Sehingga hasil test awal dan test akhir mengalami perubahan yang signifikan (berarti). Berdasarkan statistika deskriptif tes awal dan tes akhir terbukti test akhir lebih tinggi. Dapat disimpulkan pelatihan angkat dumbell dapat meningkatkan kekuatan otot.

 Penjelasan Kolom tabel Paired Samples Test

a.    Kolom pertama menunjukkan pengujian pasangan, pada contoh pada baris 1 berisi data Pair 1, jika kita melakukan pengujian dengan banyak pasangan maka baris yang dihasilkan akan lebih banyak.

b.    Mean menunjukkan rata-rata perbedaan nilai dari 2 variabel yang diuji yang merupakan selisih mean test awal dan test akhir.

c.    Std. Deviation menunjukkan standar deviasi dari skor perbedaan.

d.    Std. Error Mean menunjukkan standar error dari perbedaan nilai digunakan dalam menghitung statistik uji dan interval kepercayaan (Lower dan Upper bound).

e.    t menunjukkan statistik uji (dilambangkan dengan t) untuk uji berpasangan (paired test)

f.     df menunjukkan derajat kebebasan dari pengujian.

g.    sig (2-tailed) menunjukkan p-value atau signifikansi hasil pengujian yang bersesuaian dengan statistik uji (t) dan derajat kebebasan (df).

 Contoh Soal

1.    Apakah yang dimaksud dengan Uji t Berpasangan ?

Penyelesaian :

Uji-t berpasangan (paired t-test) adalah salah satu metode pengujian hipotesis dimana data yang digunakan tidak bebas yang dicirikan dengan adanya hubungan nilai pada setiap sampel yang sama (berpasangan).

2.    Bagaimana kriteria dalam pengujian uji-t data perpasangan?

Penyelesaian :

Kriteria data untuk uji t sampel berpasangan :

·      Data untuk tiap pasang yang diuji dalam skala interval atau rasio.

·      Data berdistribusi normal.

·      Nilai variannya dapat sama ataupun tidak

3.    Sebuah penelitian memiliki tujuan ingin mengetahui apakah terdapat perbedaan waktu yang dibutuhkan perawat untuk memasang infuse sebelum dan sesudah mengikuti pelatihan. Karena itu peneliti mengambil sampel acak terhadap 10 orang perawat. Berikut adalah waktu yang dibutuhkan seorang perawat saat memasang sebelum dan sesudah mengikuti pelatihan, data berikut dihitung dalam menit.

Penyelesaian :

4.    Seorang peneliti mempelajari pengaruh pencahayaan pada suatu tanaman bunga Lucerne pada kondisi lingkungan yang berbeda. Peneliti mengambil 10 tanaman yang segar dengan bunga-bunga yang tersinari tanpa halangan dibagian atas dan bunga bunga yang tersembunyi dibagian bawahnya. Kemudian, data banyaknya biji pada setiap lokasi dikumpulkan (Torrie, 1980).

Penyelesaian :

Uji hipotesis tidak terdapat perbedaan antara rata-rata populasi (H0) dan tandingannya (bunga yang terletak di bagian atas lebih banyak menghasilkan biji, H1). Gunakan taraf nyata 0.05.

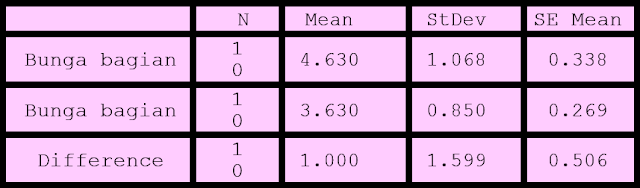
Output perhitungan dengan menggunakan Software MINITAB v.11:

Paired T-Test and CI: Bunga bagian atas, Bunga bagian bawah

Paired T for Bunga bagian atas - Bunga bagian bawah

      

Interpretasi:

Hipotesis:

1. H0: μd = 0

2. H1: μd > 0 (mengapa menggunakan tanda “>”, bandingkan dengan contoh soal Efektivitas Bimbel

dalam meningkatkan nilai ujian!)

tobs = thitung = T-Value = 1.98

tcrit = ttabel = t(0.05,9) = 1.833 (diperoleh dari nilai tabel t-student) Karena |tobs| > |tcrit| 1.98 > 1.833 maka H0 ditolak!

Artinya: 95% kita percaya bahwa bunga yang terletak di bagian atas menghasilkan biji lebih banyak dibandingkan dengan bunga yang ada di bagian bawahnya.

Metode Modern:

Metode di atas adalah uji statistik dengan metode tradisional. Uji dengan metode modern menggunakan nilai p-value dalam menentukan signifikan atau tidaknya suatu uji statistik. Apabila: P-Value < Taraf Nyata maka uji nyata atau H0 ditolak

Apabila: P-Value > Taraf Nyata maka uji tidak nyata atau H0 diterima

Pada kasus diatas, P-Value = 0.040 yang nilainya lebih kecil dibanding nilai α =0.05. Hal ini menunjukkan bahwa uji tersebut signifikan atau H0 ditolak.

Apabila nilai P-Value < 0.01, maka uji tersebut sangat signifikan!

5.    Uji pada taraf nyata 0.01, apakah terdapat perbedaan konsentrasi gula dalam nektar red clover yang disimpan selama 8 jam pada dua tekanan yang berbeda (4,4 mmHg dan 9,9 mmHg)? Data konsentrasi gula disajikan pada Tabel berikut :

Tabel Kadar Gula nektar red clover (Torrie, 1980)

Penyelesaian :

Output perhitungan dengan menggunakan Software MINITAB v.11:

Paired T-Test and CI: Tekanan 4.4 mmHg, Tekanan 9.9 mmHg

Paired T for Tekanan 4.4 mmHg - Tekanan 9.9 mmHg

99% CI for mean difference: (8.584, 13.156)

T-Test of mean difference = 0 (vs not = 0): T-Value = 15.46       P-Value = 0.000

Interpretasi:

Hipotesis:

1.    H0: μd = 0

2.    H1: μd ≠ 0

tobs = thitung = T-Value = 15.46

tcrit = ttabel = t(0.01,9) = 3.250 (dua arah pada taraf nyata 1%) Karena |tobs| > |tcrit| 15.46 > 3.250 maka H0 ditolak

Hal ini menunjukkan bahwa terdapat perbedaan yang sangat signifikan antara kedua tekanan tersebut terhadap kadar gula.

Metode Modern:

Metode   di   atas   adalah   uji   statistik   dengan  metode  tradisional.    Uji dengan metode modern menggunakan nilai p-value dalam menentukan signifikan atau tidaknya suatu uji statistik.

Apabila: P-Value < Taraf Nyata maka uji nyata atau H0 ditolak

Apabila: P-Value > Taraf Nyata maka uji tidak nyata atau H0 diterima

Pada kasus diatas, P-Value = 0.000 yang jauh lebih kecil dibanding nilai α =0.01. Hal ini berarti uji

tersebut sangat nyata.