Korelasi Bivariat dan Parsial

A.  PENGERTIAN KORELASI

Secara sederhana, korelasi dapat diartikan sebagai hubungan. Namun ketika dikembangkan lebih jauh, korelasi tidak hanya dapat dipahami sebatas pengertian tersebut. Korelasi merupakan salah satu teknik analisis dalam statistik yang digunakan untuk mencari hubungan antara dua variabel yang bersifat kuantitatif. Hubungan dua variabel tersebut dapat terjadi karena adanya hubungan sebab akibat atau dapat pula terjadi karena kebetulan saja. Dua variabel dikatakan berkolerasi apabila perubahan pada variabel yang satu akan diikuti perubahan pada variabel yang lain secara teratur dengan arah yang sama (korelasi positif) atau berlawanan (korelasi negatif).

Dalam Matematika, korelasi merupakan ukuran dari seberapa dekat dua variabel berubah dalam hubungan satu sama lain. Sebagai contoh, kita bisa menggunakan tinggi badan dan usia siswa SD sebagai variabel dalam korelasi positif. Semakin tua usia siswa SD, maka tinggi badannya pun menjadi semakin tinggi. Hubungan ini disebut korelasi positif karena kedua variabel mengalami perubahan ke arah yang sama, yakni dengan meningkatnya usia, maka tinggi badan pun ikut meningkat.  Sementara itu, kita bisa menggunakan nilai dan tingkat ketidak hadiran siswa sebagai contoh dalam korelasi negatif. Semakin tinggi tingkat ketidak hadiran siswa di kelas, maka nilai yang diperolehnya cenderung semakin rendah. Hubungan ini disebut korelasi negatif karena kedua variabel mengalami perubahan ke arah yang berlawanan, yakni dengan meningkatnya tingkat ketidak hadiran, maka nilai siswa justru menurun. Kedua variabel yang dibandingkan satu sama lain dalam korelasi dapat dibedakan menjadi variabel independen dan variabel dependen. Sesuai dengan namanya, variabel independen adalah variabel yang perubahannya cenderung di luar kendali manusia. Sementara itu variabel dependen adalah variabel yang dapat berubah sebagai akibat dari perubahan variabel indipenden. Hubungan ini dapat dicontohkan dengan ilustrasi pertumbuhan tanaman dengan variabel sinar matahari dan tinggi tanaman. Sinar matahari merupakan variabel independen karena intensitas cahaya yang dihasilkan oleh matahari tidak dapat diatur oleh manusia. Sedangkan tinggi tanaman merupakan variabel dependen karena perubahan tinggi tanaman dipengaruhi langsung oleh intensitas cahaya matahari sebagai variabel indipenden.

B.  Manfaat analisis korelasi

Analisis korelasi seringkali digunakan untuk menyatakan derajat kekuatan hubungan antara dua variabel. Dengan mengetahui hubungan antar 2 variabel, kita bisa mendeskripsikan bagaimana gambaran yang lebih bermanfaat dari data-data yang kita miliki. Korelasi seringkali digunakan dalam dunia riset ataupun bisnis.

Contohnya saja, seorang pemimpin perusahaan kerap kali menggunakan korelasi untuk mengetahui apakah terdapat hubungan yang kuat antara kenaikan gaji pegawai dengan jumlah pendapatan perusahaan. Analisis korelasi mampu menjelaskan hal ini dan memberikan analisis yang bermanfaat bagi para pengambil keputusan.

C.  Jenis hubungan korelasi

Ada 2 jenis korelasi :

1.    Korelasi positif

Korelasi positif adalah hubungan antara 2 variabel dimana kenaikan satu variabel menyebabkan penambahan nilai pada variabel lainnya. Atau sebaliknya, semakin kecil nilai suatu variabel, nilai variabel lainnya juga akan ikut turun. Bisa dikatakan juga, korelasi ini merupakan hubungan yang searah. Contohnya : penambahan usia berbanding lurus dengan penambahan tinggi badan, penambahan waktu produksi akan berbanding lurus dengan penambahan jumlah produksi. analisis-korelasi-sederhana

2.    Korelasi negatif

Korelasi negatif adalah hubungan antara 2 variabel dimana kenaikan satu variabel menyebakan penurunan nilai dari variabel lainnya. Begitu juga sebaliknya, semakin kecil nilai suatu variabel, semakin besar nilai variabel lainnya. Hubungan antara kedua variabel dalam kasus ini adalah berbalik arah.Contohnya : semakin lama waktu belajar seseorang, semakin sedikit kesalahan yang dilakukan saat ujian. Dalam pendugaan ada atau tidaknya korelasi, kita bisa mengacu kepada teori-teori yang sudah ada sebelumnya atau asumsi-asumsi yang sudah diyakini kebenarannya. Dengan teori ini, kita bisa menduga apakah terdapat korelasi antara kedua variabel atau tidak.

Misalkan saja, hubungan antara tingkat pendapatan dengan jumlah tabungan. Semakin tinggi pendapatan seseorang, semakin besar pula tabungan yang ia miliki. Atau dengan contoh lain, semakin tinggi harga suatu produk, semakin rendah daya beli masyarakat.

Bila anda menemukan data-data dengan kondisi yang sudah memiliki dasar teori seperti itu, maka tentunya anda sudah bisa mengira apakah terdapat korelasi antar variabel atau tidak. Maka langkah berikutnya yang perlu anda lakukan adalah mendeteksi hubungan korelasi tesebut dengan menggunakan metode statistik yang sudah valid.

D.  MACAM-MACAM KORELASI

Korelasi sebagai sebuah analisis memiliki berbagai jenis menurut tingkatannya. Beberapa tingkatan korelasi yang telah dikenal selama ini antara lain adalah korelasi sederhana, korelasi parsial, dan korelasi ganda. Berikut ini adalah penjelasan dari masing-masing korelasi dan bagaimana cara menghitung hubungan dari masing-masing korelasi tersebut.

1.    Korelasi Sederhana (Brivta)

Korelasi Sederhana merupakan suatu teknik statistik yang dipergunakan untuk mengukur kekuatan hubungan antara 2 variabel dan juga untuk dapat mengetahui bentuk hubungan keduanya dengan hasil yang bersifat kuantitatif. Kekuatan hubungan antara 2 variabel yang dimaksud adalah apakah hubungan tersebut erat, lemah,  ataupun tidak erat. Sedangkan bentuk hubungannya adalah apakah bentuk korelasinya linear positifataupun linear negatif. Di antara sekian banyak teknik-teknik pengukuran asosiasi, terdapat dua teknik korelasi yang sangat populer sampai sekarang, yaitu Korelasi Pearson Product Moment dan Korelasi Rank Spearman. Lalu apa perbedaan di antara keduanya? Korelasi Pearson Product Moment adalah korelasi yang digunakan untuk data kontinu dan data diskrit. Korelasi pearson cocok digunakan untuk statistik parametrik. Ketika data berjumlah besar dan memiliki ukuran parameter seperti mean dan standar deviasi populasi.

Korelasi Pearson menghitung korelasi dengan menggunakan variasi data. Keragaman data tersebut dapat menunjukkan korelasinya. Korelasi ini menghitung data apa adanya, tidak membuat ranking atas data yang digunakan seperti pada korelasi Rank Spearman. Ketika kita memiliki data numerik seperti nilai tukar rupiah, data rasio keuangan, tingkat pertumbuhan ekonomi, data berat badan dan contoh data numerik lainnya, maka Korelasi Pearson Product Moment cocok digunakan.  Sebaliknya, Koefisien Korelasi Rank Spearman digunakan untuk data diskrit dan kontinu namun untuk statistik nonparametrik. Koefisien korelasi Rank Spearman lebih cocok untuk digunakan pada statistik nonparametrik. Statistik nonparametrik adalah statistik yang digunakan ketika data tidak memiliki informasi parameter, data tidak berdistribusi normal atau data diukur dalam bentuk ranking. Berbeda dengan Korelasi Pearson, korelasi ini tidak memerlukan asumsi normalitas, maka korelasi Rank Spearman cocok juga digunakan untuk data dengan sampel kecil.

Korelasi Rank Spearman menghitung korelasi dengan menghitung ranking data terlebih dahulu. Artinya korelasi dihitung berdasarkan orde data. Ketika peneliti berhadapan dengan data kategorik seperti kategori pekerjaan, tingkat pendidikan, kelompok usia, dan contoh data ketegorik lainnya, maka Korelasi Rank Spearman cocok digunakan. Korelasi Rank Spearman pun cocok digunakan pada kondisi dimana peneliti dihadapkan pada data numerik (kurs rupiah, rasio keuangan, pertumbuhan ekonomi), namun peneliti tidak memiliki cukup banyak data (data kurang dari 30).

Koefisien Korelasi Sederhana disebut juga dengan Koefisien Korelasi Pearson karena rumus perhitungan Koefisien korelasi sederhana ini dikemukakan oleh Karl Pearson yaitu seorang ahli Matematika yang berasal dari Inggris. Rumus yang dipergunakan untuk menghitung Koefisien Korelasi Sederhana adalah sebagai berikut :

Persyaratan Dalam Analisis Korelasi Bivariate Pearson

Ada beberapa persyaratan atau asumsi dasar yang harus terpenuji ketika kita hendak memakai analisis korelasi bivariate pearson untuk menguji hipotesis penelitian kita.

·      Data penelitian untuk masing-masing variabel setidak-tidaknya berskala rasio atau interval (yaitu data yang berbentuk angka sesungguhnya atau data metrik (data kuantitatif). Naun demikian analisis ini biasanya dipakai untuk data kuesioner dan skala likert

·      Data untuk masing-masing variabel yang dihubungkan berdistribusi normal

·      Terdapat hubungan yang linier antar variabel penelitian

Arti Angka Korelasi (Pearson Correlations)

Koefisien korelasi atau pearson correlation memiliki nilai paling kecil -1 dan paling besar 1.

·      Berkenaan dengan besaran angka ini, jika 0 maka artinya tidak ada korelasi sama sekali sementara jika korelasi 1 maka ada korelasi sempurna. Hal ini menunjukkan bahwa semakin nilai pearson correlation mendekati 1 atau -1 maka hubungan antara dua variabel adalah semakin kuat. Sebaliknya, jika nilai r atau Pearson Correlation mendekati 0 berarti hubungan dua variabel menjadi semakin lama. Sebenarnya tidak ada ketentuan yang benar-benar tepat mengenai apakah angka korelasi tertentu menunjukkan tingkat korelasi yang tinggi atau lemah. Namun, hal berikut ini dapat jadikan pedoman sederhana bahwa jka angka korelasi diatas 0,5 akan menunjukkan korelasi yang cukup kuat sedangkan jika dibawah 0,5 maka menunjukkan korelasi yang lemah.

·      Selain besarnya korelasi, tanda korelasi juga berpengaruh pada penafsiran hasil dalam analisis ini. Dimana, tanda negatif (-) pada tabel output SPSS menunjukkan adanya arah yang berlawanan, sedangkan tanda positif (+) menunjukkan arah yang sama atau korelasi searah.

  Dasar Keputusan Dalam Analisis Korelasi Bivariate Pearson

Terdapat 3 cara yang dapat digunakan sebagai pedoman atau dasar pengambilan keputusan dalam analisis korelasi bivariate pearson ini yaitu pertama dengan melihat nilai signifikan Sig. (2 tailed). Kedua membandingkan nilai r hitung (Pearson Correlation) dengan nilai r tabel product momen. Ketiga adalah dengan melihat tanda bintang (*) yang terdapat pada output program SPSS.

·      Berdasarkan nilai signifikan Sig (2-tailed) : jika nilai Sig (2-tailed) < 0,05 maka terdapat korelasi antar variabel yang dihubungkan. Sebaliknya jika nilai Sig (2-tailed) > 0,05 maka tidak terdapat korelasi.

·      Berdasarkan nilai r hitung (Pearson Correlation) : jika nilai r hitung > r tabel maka ada korelasi antar variabel. Sebaliknya jika nilai r hitung  r tabel maka artinya tidak ada korelasi antar variabel.

·      Berdasarkan tanda bintang (*) yang diberikan SPSS : jika terdapat tanda bintang (*) atau (**) pada nilai Pearson Correlation maka antara variabel yang dianalisis terjadi korelasi. Sebaliknya jika tidak terdapat tanda bintang pada nilai pearson correlation maka antara variabel yang dianalisis tidak terjadi korelasi.

Catatan: Tanda bintang satu (*) menunjukkan korelasi pada signifikansi 1% atau 0,01. Sedangkan tanda bintang dua (**) menunjukkan korelasi pada signifikansi 5% atau 0,05.

2.    Korelasi Parsial

Korelasi parsial adalah suatu metode pengukuran keeratan hubungan (korelasi) antara variabel bebas dan variabel tak bebas dengan mengontrol salah satu variabel bebas untuk melihat korelasi natural antara variabel yang tidak terkontrol. Analisis korelasi parsial (partial correlation) melibatkan dua variabel. Satu buah variabel yang dianggap berpengaruh akan dikendalikan atau dibuat tetap (sebagai variabel kontrol).

Sebagai contoh misalnya kita akan meneliti hubungan variabel X2 dan variabel bebas Y, denganX1 dikontrol (korelasi parsial). Disini variabel yang dikontrol (X1) dikeluarkan atau dibuat konstan. Sehingga X2’ = X2 – (b2X1 + a2 ) dan Y’ = Y – (b1 X1 +a1 ), tetapi nilai a dan b didapatkan dengan menggunakan regresi linear. Setelah hasilnya diperoleh, kemudian dicari regresi X2‘ dengan Y’ dimana : Y’ = b3X2’ +a3. Korelasi yang didapatkan dan sejalan dengan model-model di atas dinamakan korelasi parsial X2 dan Y sedangkan X1 dibuat konstan.

Nilai korelasi berkisar antara 1 sampai -1, nilai semakin mendekati 1 atau -1 berarti hubungan antara dua variabel semakin kuat. Sebaliknya, jika nilai mendekati 0 berarti hubungan antara dua variabel semakin lemah. Nilai positif menunjukkan hubungan searah (X naik, maka Y naik) sementara nilai negatif menunjukkan hubungan terbalik (X naik, maka Y turun).  Data yang digunakan dalam korelasi parsial biasanya memiliki skala interval atau rasio. Berikut adalah pedoman untuk memberikan interpretasi serta analisis bagi koefisien korelasi menurut Sugiyono:

·      - 0,199 = sangat rendah

·      0,20 - 0,3999 = rendah

·      0,40 - 0,5999 = sedang

·      0,60 - 0,799 = kuat

·      0,80 - 1,000 = sangat kuat

Mengontrol suatu variable sangat berguna karena itu sebaiknya kita dapat mengerjakanny adengan cepat.   Rumus sederhana untuk menghitung korelasi parsial :

Korelasi parsia ldigunakan untuk mencari arah dan kuat lemahnya hubungan antara 2 atau lebih variable independen        (X1,X2...Xn)   terhadap          variable            dependen (Y) secarabersamaan , dengan mengendalikan salah satu variabel independenya.

Koefisien Determinasi

Koefisien korelasi r,      hanya menyediakan ukuran kekuatan dan arah hubungan

linier antaraduavariabel. Akan tetapi tidak memberikan informasi mengenai berapa proporsi keragaman (variasi) variabel dependen (Y) yang dapat diterangkan atau diakibatkan oleh hubungan linier dengan nilai variabel independen (X). Koefisien Determinasi bisa di definisikan sebagai nilai yang menyatakan proporsi keragaman Y yang dapat diterangkan/dijelaskan oleh hubungan linier antara variabel X dan Y. Untuk menentukan besar kecilnya sumbangan variabel X terhadap Y dapat ditentukan dengan rumus koefisien determinan sebagai berikut :

KP = r2 x 100%

Dimana :

KP adalah besarnya koefisien penentu (diterminan) r adalah koefisien korelasi

Cari Koefisien parsial, jika X1 tetap.

Analisis Korelasi Parsial

a.    Jika X1 tetap maka :

Hepotesa :

Ha : Ada pengaruh yang signifikan antara X2 dan Y jika X1 tetap.

H0 : Tidak ada pengaruh yang signifikan antara X2 dan Y jika X1 tetap.

b.    Jika X2 tetap maka :

Hepotesa :

Ha : Ada pengaruh yang signifikan antara X1 dan Y jika X2 tetap

H0 : Tidak ada pengaruh yang signifikan antara X1 dan Y jika X2 tetap Untuk uji signifikansinya menggunakan rumus :

Keterangan:

thitung          = nilai yang akan dibandingkan dengan ttabel rpar    = nilai koefisien parsial

n        = jumlah sample Kriteria pengujian :

thitung ≥ ttabel ; maka tolak H0 (signifikan)

thitung < ttabel ; maka terima H0 (tidak signifikan) db ttabel = n-1

3.    Korelasi Ganda

Korelasi ganda adalah bentuk korelasi yang digunakan untuk melihat hubungan antara tiga atau lebih variabel (dua atau lebih variabel independen dan satu variabel dependent. Korelasi ganda berkaitan dengan interkorelasi variabel-variabel independen sebagaimana korelasi mereka dengan variabel dependen.

Korelasi ganda adalah suatu nilai yang memberikan kuatnya pengaruh atau hubungan dua variabel atau lebih secara bersama-sama dengan variabel lain. Korelasi ganda merupakan korelasi yang terdiri dari dua atau lebih variabel bebas (X1,X2,…..Xn) serta satu variabel terikat (Y). Apabila perumusan masalahnya terdiri dari tiga masalah, maka hubungan antara masing-masing variabel dilakukan dengan cara perhitungan korelasi sederhana.  Korelasi ganda memiliki koefisien korelasi, yakni besar kecilnya hubungan antara dua variabel yang dinyatakan dalam bilangan. Koefisien Korelasi disimbolkan dengan huruf R. Besarnya Koefisien Korelasi adalah antara -1; 0; dan +1.  Besarnya korelasi -1 adalah negatif sempurna yakni terdapat hubungan di antara dua variabel atau lebih namun arahnya terbalik, +1 adalah korelasi yang positif sempurna (sangat kuat) yakni adanya sebuah hubungan di antara dua variabel atau lebih tersebut, sedangkan koefisien korelasi 0 dianggap tidak terdapat hubungan antara dua variabel atau lebih yang diuji sehingga dapat dikatakan tidak ada hubungan sama sekali.

E.   Uji Korelasi dengan SPSS

a.    Korelasi Brivate

Misalkan saya ingin menguji apakah ada hubungan yang signifikan antara Motivasi dan Minat dengan Prestasi belajar siswa. Adapun detail data penelitiannya dapat anda lihat di bawah ini.

Langkah-langkahnya yaitu :

1.    Buka program SPSS, klik Variable View. Selanjutnya, pada bagian Name tulis saja X1, X2 dan Y, pada Decimals ubah semua menjadi angka 0, pada bagian Label tuliskan Motivasi, Minat dan Prestasi. Pada bagian Measure ganti menjadi Scale

2.    Setelah itu, klik Data View, dan masukkan data Motivasi (X1), Minat (X2) dan Prestasi (Y) yang sudah dipersiapkan tadi ke program SPSS.

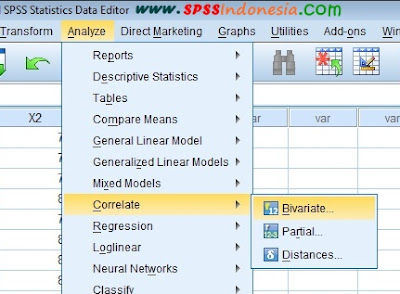
3.    Selanjutnya, dari menu utama SPSS, pilih menu Analyze, lalu klik Correlate, dan klik Bivariate...

Cara Melakukan Analisis Korelasi Bivariate Pearson dengan SPSS

Muncul kotak dialog dengan nama "Bivariate Correlations". Masukkan variabel Motivasi (X1), Minat (X2) dan Prestasi (Y) pada kotak Variables:. Selanjutnya, pada kolom "Correlation Coefficient" pilih Pearson, lalu untuk kolom "Test of Significant" pilih Two-tailed, dan centang pada Flag Significant Correlations, terakhir klik Ok untuk mengakhiri perintah.

Setelah selasai, maka akan muncul tampilan output SPSS "Correlations" tinggal kita interpretasikan saja.

Interpretasi Analisis Korelasi Bivariate Pearson

Berdasarkan tabel output di atas, kita akan melakukan pernarikan kesimpulan dengan merujuk pada ke-3 dasar pengambilan keputusan dalam analisis korelasi bivariate pearson di atas.

1.    Berdasarkan Nilai Signifikansi Sig. (2-tailed): Dari tabel output di atas diketahui nilai Sig. (2-tailed) antara Motivasi (X1) dengan Prestasi (Y) adalah sebesar 0,002 < 0,05, yang berarti terdapat korelasi yang signifikan antara variabel Motivasi dengan variabel Prestasi. Selanjutnya, hubungan antara Minat (X2) dengan Prestasi (Y) memiliki nilai Sig. (2-tailed) sebesar 0,000 < 0,05, yang berarti terdapat korelasi yang signifikan antara variabel Minat dengan variabel Prestasi.

2.    Berdasarkan Nilai r hitung (Pearson Correlations): Diketahui nilai r hitung untuk hubungan Motivasi (X1) dengan Prestasi (Y) adalah sebesar adalah sebesar 0,796 > r tabel 0,576, maka dapat disimpulkan bahwa ada hubungan atau korelasi antara variabel Motivasi dengan variabel Prestasi. Selanjutnya, diketahui nilai r hitung untuk hubungan Minat (X2) dengan Prestasi (Y) adalah sebesar adalah sebesar 0,908 > r tabel 0,576, maka dapat disimpulkan bahwa ada hubungan atau korelasi antara variabel Minat dengan variabel Prestasi. Karena r hitung atau Pearson Correlations dalam analisis ini bernilai positif maka itu artinya hubungan antara kedua variabel tersebut bersifat positif atau dengan kata lain semakin meningkatnya Motivasi dan Minat maka akan meningkat pula Prestasi belajar siswa.

Catatan: Rumus menghitung nilai r tabel product moment adalah dengan melihat nilai N pada distribusi nilai r tabel product moment statistik. Karena N atau jumlah sampel yang digunakan dalam analisis ini ada 12 orang siswa dengan signifikansi 5% maka ketemu nilai r tabel adalah sebesar 0,576. lihat gambar di bawah ini.

3.      Berdasarkan Tanda Bintang (*) SPSS: Dari output di atas diketahui bahwa nilai Pearson Correlation antara masing-masing variabel yang dihubungkan mempunyai dua tanda bintang (**), ini berarti terdapat korelasi antara variabel yang dihubungkan dengan taraf signifikansi 1%.

b.    Korelasi Parsial

Seorang dosen ingin mengetahui apakah ada hubungan antara IQ (Intelligence Quotient) dengan nilai IPK (Indeks Prestasi Kumulatif) mahasiswa dengan Motivasi Berprestasi sebagai variabel Kontrol. Guna keperluan penelitian ini maka dosen tersebut mengumpulkan data-data yang dibutuhkan menggunakan kuesioner untuk 12 orang sampel atau responden penelitian. Adapun tabulasi data penelitian yang dimaksud dapat anda lihat pada tabel berikut ini.

tahapan-tahapan analisis data dalam uji korelasi parsial ini dimulai dari memasukkan atau menginput data penelitian ke program SPSS, selanjutnya melakukan uji normalitas data terlebih dahulu, baru kemudian melakukan analisis data dengan uji korelasi parsial.

1.    Langkah pertama buka lembar kerja baru SPSS, lalu klik Variable View, selanjutnya anda cukup mengisi pada kolom Name, Decimals, Label, dan Measure, sementara untuk pilihan yang lain biarkan tetap default. Tampak di layar SPSS sebagaimana gambar bawah ini.

2.    Jika sudah, langkah berikutnya klik Data View, lalu masukkan data IQ, IPK dan Motivasi ke-12 orang responden tersebut sesuai dengan judul kolom yang ada di layar SPSS.

*Melakukan Uji Normalitas Data Penelitian dengan SPSS

Karena persyaratan atau asumsi dasar yang harus terpenuhi dalam penggunaan uji korelasi parsial ini adalah data berdistribusi normal, maka terlebih dahulu kita akan melakukan uji normalitas untuk variabel IQ, IPK dan Motivasi. Adapun caranya sebagai berikut ini.

1.    Dari menu utama SPSS klik menu Analyze >> Descriptive Statistics >> Explore…

2.    Maka muncul kotak dialog “Explore” selanjutnya masukkan semua variabel penelitian ke kotak Dependent List: kemudian pada bagian “Display” pilih Both, setelah itu klik Plots…

3.    Maka muncul kotak dialog “Explore Plots” lalu beri tanda ceklist (v) pada Normality plots with tests, selanjutnya klik Continue, kemudian klik Ok

4.    Maka akan mucul output SPSS, kita cukup perhatikan pada tabel output “Tests of Normality” tampak dilayar seperti gambar di bawah ini.

*Pembahasan Uji Normalitas untuk Uji Korelasi Parsial dengan SPSS

Untuk mengetahui apakah variabel IQ, IPK dan Motivasi yang digunakan dalam penelitian berdistribusi normal atau tidak, maka terlebih dahulu kita harus mengetahui teori tentang dasar pengambilan keputusan untuk uji normalitas. Adapun dasar pengambilan keputusan dalam uji normalitas adalah sebagai berikut.

a.    Jika nilai Signifikansi (Sig.) < 0,05, maka variabel tidak berdistribusi normal.

b.    Jika nilai Signifikansi (Sig.) > 0,05, maka variabel berdistribusi normal.

Berdasarkan tabel output SPSS “Tests of Normality” di atas, diketahui bahwa nilai Sig. dalam uji normalitas Shapiro-Wilk adalah sebagai berikut.

Nilai IQ Sig. adalah sebesar 0,932

a.    Nilai IPK Sig. adalah sebesar 0,152

b.    Nilai Motivasi Sig. adalah sebesar 0,066

Karena nilai signifikansi (Sig.) untuk semua variabel penelitian di atas > 0,05 maka dapat disimpulkan variabel IQ, IPK dan Motivasi adalah berdistribusi normal. Dengan demikian, asumsi dasar atau persyaratan dalam uji korelasi parsial sudah terpenuhi.

Catatan: metode Shapiro-Wilk dipakai untuk sampel < 50. Sementara metode Kolmogorov-Smirnov dipakai untuk sampel > 50.

Melakukan Uji Korelasi Parsial dengan SPSS

1.    Selanjutnya kita akan melakukan Uji Korelasi Parsial dengan SPSS, caranya klik menu Analyze >> Correlate >> Partial… Tampak dilayar.

2.    Muncul kotak dialog “Partial Correlations” Selanjutnya, masukkan variabel IQ dan IPK ke kotak Variables: kemudian masukkan variabel Motivasi ke kotak Controlling for, pada bagian “Test of Significance” pilih Two-tailed dan beri tanda ceklist (v) untuk Display actual significance level, lalu klik Options…

3.    Muncul kotak diloag “Partial Correlations: Options”, kemudian pada bagian “Statistics” berikan tanda ceklist (v) untuk Means and standard deviations dan Zero-order correlations. Selanjutnya pada bagian “Missing Values” aktifkan pilihan Exclude cases pairwise, lalu klik Continue

4.    Kemudian klik Ok untuk mengakhiri perintah. Maka muncul Output SPSS dengan judul “Partial Corr” selanjutnya tinggal interpretasikan saja tabel output tersebut.

Interpretasi Output Uji Korelasi Parsial dengan SPSS

Tabel Output “Descriptive Statistics”

Tabel output SPSS di atas, memberikan informasi kepada kita tentang ringkasan nilai statistik deskriptif atau gambaran data untuk ketiga variabel (IQ, IPK dan Motivasi) mencakup Mean atau nilai rata-rata, Std. Deviation (Standar Deviasi), dan N atau jumlah sampel yang digunakan dalam penelitian ini.

Tabel Output “Correlations”

Tabel output SPSS ini memberikan informasi mengenai hubungan yang terbentuk antar variabel sebelum dan sesudah dimasukkannya variabel kontrol dalam analisis korelasi. Untuk memaknai tabel output Correlations di atas, maka ada 3 tahapan yang harus kita lalui, yaitu: (1) Menentukan rumusan hipotesis penelitian. (2) Melihat teori tentang dasar pengambilan keputusan dalam uji korelasi parsial. (3) Manafsirkan hasil analisis dan membuat kesimpulan.

*Rumusan Hipotesis Penelitian dalam Uji Korelasi Parsial

a.    H0: Hubungan antara IQ dengan IPK dengan Motivasi sebagai variabel kontrol tidak signifikan.

b.    Ha: Hubungan antara IQ dengan IPK dengan Motivasi sebagai variabel kontrol signifikan.

*Dasar Pengambilan Keputusan dalam Uji Korelasi Parsial Sig. (2-tailed)

a.    Jika nilai Significance (2-tailed) > 0,05, maka H0 diterima dan Ha ditolak.

b.    Jika nilai Significance (2-tailed) < 0,05, maka H0 ditolak dan Ha diterima.

*Pembahasan Output Uji Korelasi Parsial dengan SPSS

Tabel output pertama “-none-a” menunjukkan nilai korelasi atau hubungan antara variabel IQ dengan IPK sebelum dimasukkannya variabel kontrol (Motivasi) dalam analisis. Dari output di atas diketahui nilai koefisien korelasi (Correlations) sebesar 0,832 (positif) dan nilai Significance (2-tailed) adalah 0,001 < 0,05, maka dapat disimpulkan bahwa ada hubungan yang positif dan signifikan antara IQ dengan IPK mahasiswa tanpa adanya variabel kontrol (Motivasi). Sementara nilai Correlations sebesar 0,832 ini masuk dalam kategori hubungan sangat kuat.

Tabel output kedua “Motivasi” menujukkan nilai korelasi atau hubungan antara variabel IQ dengan IPK setelah memasukkan Motivasi sebagai variabel kontrol dalam analisis. Dari tabel output di atas terlihat bahwa terjadi penurunan nilai koefisien korelasi (Correlations) menjadi 0,626 (bernilai positif dan kategori hubungan kuat) dengan nilai Significance (2-tailed) sebesar 0,039 < 0,05, maka H0 ditolak dan Ha diterima yang berarti bahwa hubungan antara IQ dengan IPK dengan Motivasi sebagai variabel kontrol adalah signifikan (nyata).

*Kesimpulan Penelitian

Berdasarkan pembahasan dalam uji korelasi parsial di atas diketahui bahwa kehadiran variabel motivasi berprestasi sebagai variabel kontrol akan memberikan pengaruh terhadap hubungan antara variabel IQ dengan variabel IPK. Dengan demikian maka dapat disimpulkan bahwa variabel IQ (Intelligence Quotient) bukanlah satu-satunya variabel yang menentukan nilai IPK mahasiswa, karena ada variabel lain juga yang berhubungan dengan nilai IPK yaitu variabel Motivasi berprestasi.

Contoh Soal

1.    Apakah yang dimaksud dengan kolerasi ?

Penyelesaian :

Secara sederhana, korelasi dapat diartikan sebagai hubungan. Namun ketika dikembangkan lebih jauh, korelasi tidak hanya dapat dipahami sebatas pengertian tersebut. Korelasi merupakan salah satu teknik analisis dalam statistik yang digunakan untuk mencari hubungan antara dua variabel yang bersifat kuantitatif. Hubungan dua variabel tersebut dapat terjadi karena adanya hubungan sebab akibat atau dapat pula terjadi karena kebetulan saja. Dua variabel dikatakan berkolerasi apabila perubahan pada variabel yang satu akan diikuti perubahan pada variabel yang lain secara teratur dengan arah yang sama (korelasi positif) atau berlawanan (korelasi negatif).

2.    Apkah perbedaan antara Korelasi Pearson Product Moment dan Korelasi Rank Spearman ?

Penyelesaian :

Korelasi Pearson Product Moment adalah korelasi yang digunakan untuk data kontinu dan data diskrit. Korelasi pearson cocok digunakan untuk statistik parametrik. Ketika data berjumlah besar dan memiliki ukuran parameter seperti mean dan standar deviasi populasi.

Korelasi Pearson menghitung korelasi dengan menggunakan variasi data. Keragaman data tersebut dapat menunjukkan korelasinya. Korelasi ini menghitung data apa adanya, tidak membuat ranking atas data yang digunakan seperti pada korelasi Rank Spearman. Ketika kita memiliki data numerik seperti nilai tukar rupiah, data rasio keuangan, tingkat pertumbuhan ekonomi, data berat badan dan contoh data numerik lainnya, maka Korelasi Pearson Product Moment cocok digunakan. Sebaliknya, Koefisien Korelasi Rank Spearman digunakan untuk data diskrit dan kontinu namun untuk statistik nonparametrik. Koefisien korelasi Rank Spearman lebih cocok untuk digunakan pada statistik nonparametrik. Statistik nonparametrik adalah statistik yang digunakan ketika data tidak memiliki informasi parameter, data tidak berdistribusi normal atau data diukur dalam bentuk ranking. Berbeda dengan Korelasi Pearson, korelasi ini tidak memerlukan asumsi normalitas, maka korelasi Rank Spearman cocok juga digunakan untuk data dengan sampel kecil.  Korelasi Rank Spearman menghitung korelasi dengan menghitung ranking data terlebih dahulu. Artinya korelasi dihitung berdasarkan orde data. Ketika peneliti berhadapan dengan data kategorik seperti kategori pekerjaan, tingkat pendidikan, kelompok usia, dan contoh data ketegorik lainnya, maka Korelasi Rank Spearman cocok digunakan. Korelasi Rank Spearman pun cocok digunakan pada kondisi dimana peneliti dihadapkan pada data numerik (kurs rupiah, rasio keuangan, pertumbuhan ekonomi), namun peneliti tidak memiliki cukup banyak data (data kurang dari 30).

3.    Seorang mahasiswa bernama Andi melakukan penelitian dengan menggunakan alat ukur skala. Andi ingin mengetahui apakah ada hubungan antara kecerdasan dengan prestasi belajar pada siswa SMU Negeri 1 Yogyakarta, dengan ini Andi membuat 2 variabel yaitu kecerdasan dan prestasi belajar. Tiap-tiap variabel dibuat beberapa butir pertanyaan dengan menggunakan skala Likert, yaitu angka 1 = Sangat tidak setuju, 2 = Tidak setuju, 3 = Setuju dan 4 = Sangat Setuju. Setelah membagikan skala kepada 12 responden didapatlah skor total item-item yaitu sebagai berikut:

Penyelesaian :

Langkah-langkah pada program SPSS

a.    Masuk program SPSS

b.    Klik variable view pada SPSS data editor

c.    Pada kolom Name ketik x, kolom Name pada baris kedua ketik y.

d.    Pada kolom Decimals ganti menjadi 0 untuk variabel x dan y

e.    Pada kolom Label, untuk kolom pada baris pertama ketik Kecerdasan, untuk kolom pada baris kedua ketik Prestasi Belajar.

f.     Untuk kolom-kolom lainnya boleh dihiraukan (isian default)

g.    Buka data view pada SPSS data editor, maka didapat kolom variabel x dan y.

h.    Ketikkan data sesuai dengan variabelnya

i.      Klik Analyze - Correlate - Bivariate

j.      Klik variabel Kecerdasan dan masukkan ke kotak Variables, kemudian klik variabel Prestasi Belajar dan masukkan ke kotak yang sama (Variables).

k.    Klik OK, maka hasil output yang didapat adalah sebagai berikut:

                  Tabel. Hasil Analisis Korelasi Bivariate Pearson

Dari hasil analisis korelasi sederhana (r) didapat korelasi antara kecerdasan dengan prestasi belajar (r) adalah 0,766. Hal ini menunjukkan bahwa terjadi hubungan yang kuat antara kecerdasan dengan prestasi belajar. Sedangkan arah hubungan adalah positif karena nilai r positif, berarti semakin tinggi kecerdasan maka semakin meningkatkan prestasi belajar.

-     Uji Signifikansi Koefisien Korelasi Sederhana (Uji t)

Uji signifikansi koefisien korelasi digunakan untuk menguji apakah hubungan yang terjadi itu berlaku untuk populasi (dapat digeneralisasi). Misalnya dari kasus di atas populasinya adalah siswa SMU Negeri 1 Yogyakarta dan sampel yang diambil dari kasus di atas adalah 12 siswa SMU Negeri 1 Yogyakarta, jadi apakah hubungan yang terjadi atau kesimpulan yang diambil dapat berlaku untuk populasi yaitu seluruh siswa SMU Negeri 1 Yogyakarta. Langkah-langkah pengujian sebagai berikut:

a.    Menentukan Hipotesis

Ho : Tidak ada hubungan secara signifikan antara kecerdasan dengan prestasi belajar

Ha : Ada hubungan secara signifikan antara kecerdasan dengan prestasi belajar

b.    Menentukan tingkat signifikansi

Pengujian menggunakan uji dua sisi dengan tingkat signifikansi a = 5%. (uji dilakukan 2 sisi karena untuk mengetahui ada atau tidaknya hubungan yang signifikan, jika 1 sisi digunakan untuk mengetahui hubungan lebih kecil atau lebih besar). Tingkat signifikansi dalam hal ini berarti kita mengambil risiko salah dalam mengambil keputusan untuk menolak hipotesa yang benar sebanyak-banyaknya 5% (signifikansi 5% atau 0,05 adalah ukuran standar yang sering digunakan dalam penelitian)

c.    Kriteria Pengujian

Ho diterima jika Signifikansi > 0,05

Ho ditolak jika Signifikansi < 0,05

d.    Membandingkan signifikansi

Nilai signifikansi 0,004 < 0,05, maka Ho ditolak.

e.    Kesimpulan

Oleh karena nilai Signifikansi (0,004 < 0,05) maka Ho ditolak, artinya bahwa ada hubungan secara signifikan antara kecerdasan dengan prestasi belajar. Karena koefisien korelasi nilainya positif, maka berarti kecerdasan berhubungan positif dan signifikan terhadap pretasi belajar. Jadi dalam kasus ini dapat disimpulkan bahwa kecerdasan berhubungan positif terhadap prestasi belajar pada siswa SMU Negeri 1 Yogyakarta.

4.    Penelitian dengan menggunakan alat ukur skala. Peneliti ingin mengetahui apakah ada hubungan antara kecerdasan dengan prestasi belajar pada siswa SMU Negeri 1 Yogyakarta, dengan ini Peneliti membuat 2 variabel yaitu kecerdasan dan prestasi belajar. Tiap-tiap variabel dibuat beberapa butir pertanyaan dengan menggunakan skala Likert, yaitu angka 1 = Sangat tidak setuju, 2 = Tidak setuju, 3 = Setuju dan 4 = Sangat Setuju. Setelah membagikan skala kepada 12 responden didapatlah skor total item-item yaitu sebagai berikut:

     Tabel. Tabulasi Data (Data Fiktif)

No	kecerdasan (X1)	Prestasi Belajar (X2)
1	33	58
2	32	52
3	21	48
4	34	49
5	34	52
6	35	57
7	32	55
8	21	50
9	21	48
10	35	54
11	36	56
12	21	47

Penyelesaian :

Sebelum dilakukan analisis bivariat, hal yang pertama dilakukan adalah menguji bahwa data tersebut normal. Untuk itu digunakan software SPSS dan diperoleh hasil sebagai berikut :

Output software SPSS di atas menunjukkan bahwa nilai signifikan sebesar 0,2 hal itu menunjukkan bahwa nilai signifikan lebih besar dari alfa 0,05. Berdasarkan itu dapat simpulkan bahwa populasi tersebut memiliki data yang berdistribusi normal. Langkah selanjutnya adalah melakukan pengujian analisis bivariat terhadap data tersebut. Analisis bivariat yang digunakan adalah uji Pearson’s Product Moment. Dengan menggunakan software SPSS diperoleh hasil sebagai berikut :

Dari hasil analisis korelasi sederhana didapat korelasi antara kecerdasan dengan prestasi belajar adalah 0,766 atau P-value > 0,05. Hal ini menunjukkan bahwa terjadi hubungan yang kuat antara kecerdasan dengan prestasi belajar. Sedangkan arah hubungan adalah positif karena nilai r (korelasi) positif, berarti semakin tinggi kecerdasan maka semakin meningkatkan prestasi belajar.

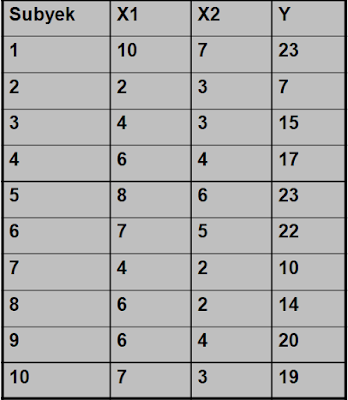
5.    Bagaimana  hubungan murni  antara X1 dan X2  terhadap Y

Penyelesaian :